Het antwoord was evenveel, dat konden we uitrekenen, maar we hadden er nog geen aansprekend en veelzeggend plaatje bij. Dat wilden we juist zo graag hebben, want dan zie je de kracht van "visual representation" waar Lean zo de nadruk op legt. Niet allen met visual management of bij problemsolving, maar ook bijvoorbeeld een 'barashi' om een visie uit te dragen.
Als je naar onderstaand diagram kijkt, dan zie je dat het totale volume in het vat A ongewijzigd is gebleven. Dat klopt natuurlijk, want er is eerst twee liter uitgeschept en daarna weer twee liter ingeschept. In vat B zit dus ook voor en na het scheppen evenveel vloeistof.
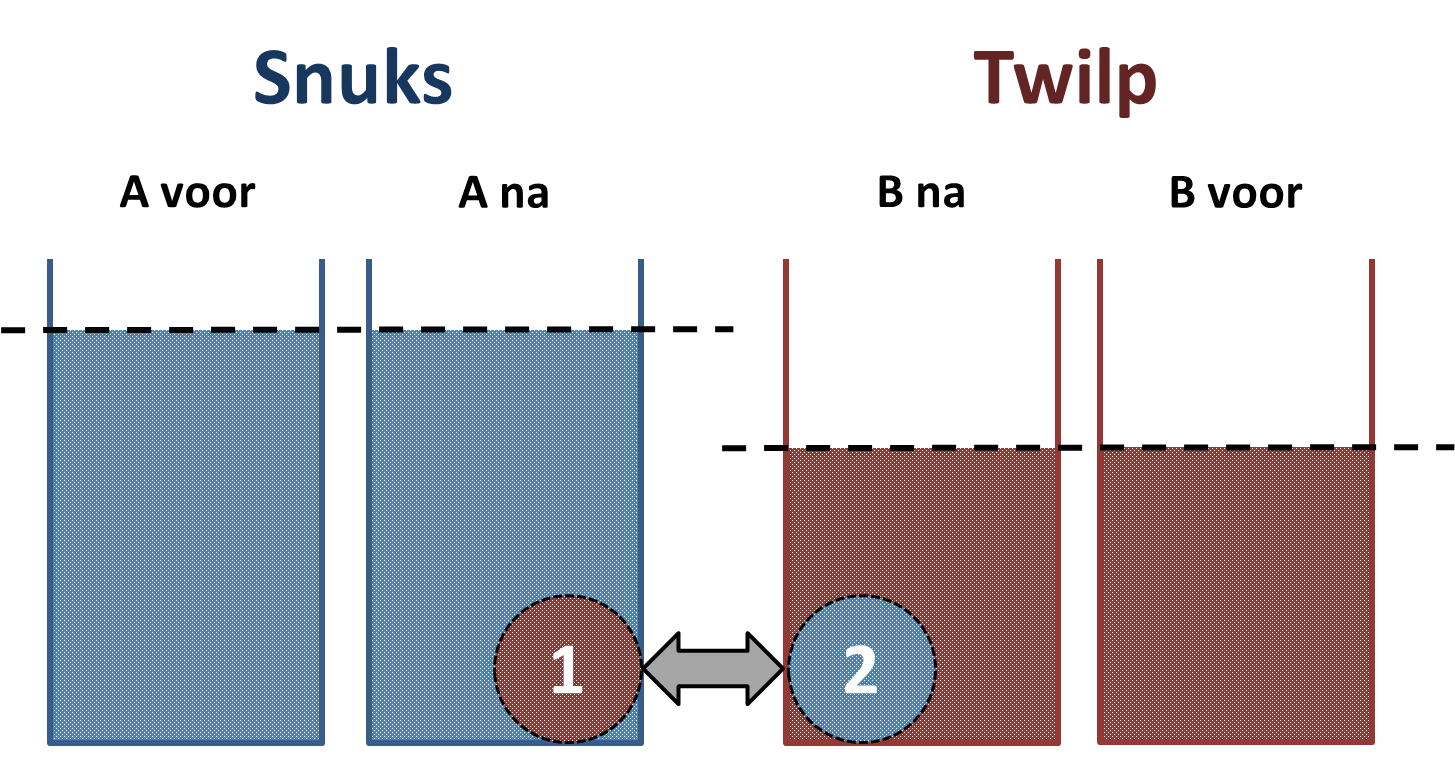
Stel nu dat we alle Twilp die in vat A terecht is gekomen zouden kunnen concentreren in een bolletje (1). Dit bolletje neem natuurlijk een bepaald volume in. Om plaats te maken voor dat volume moet een bolletje Snuks van precies dezelfde omvang zijn verdwenen. Doordat er 2 liter is uitgeschept en weer 2 liter is teruggeschept, is het totale volume in A is immers niet gewijzigd. Dat volume van dat bolletje is natuurlijk in B terecht gekomen (2).
Het leuke is nu dat je direct ziet dat dit ALTIJD opgaat. Of je nu vaten met een ander volume hebt, of je meer of minder heen en weer schept, of je nu roert of niet, het maakt allemaal niet uit. Omdat het totale volume in een vat gelijkt blijft, moet er precies evenveel van de ene stof zijn uitgegaan als er van de ander is bijgekomen. Dat is in dit geval de extra kracht van visuele representatie.
